Ethiopian News, Current Affairs and Opinion Forum
-
MINILIK SALSAWI
- Member+
- Posts: 9499
- Joined: 24 Aug 2012, 12:02
Post
by MINILIK SALSAWI » 07 Sep 2021, 03:23
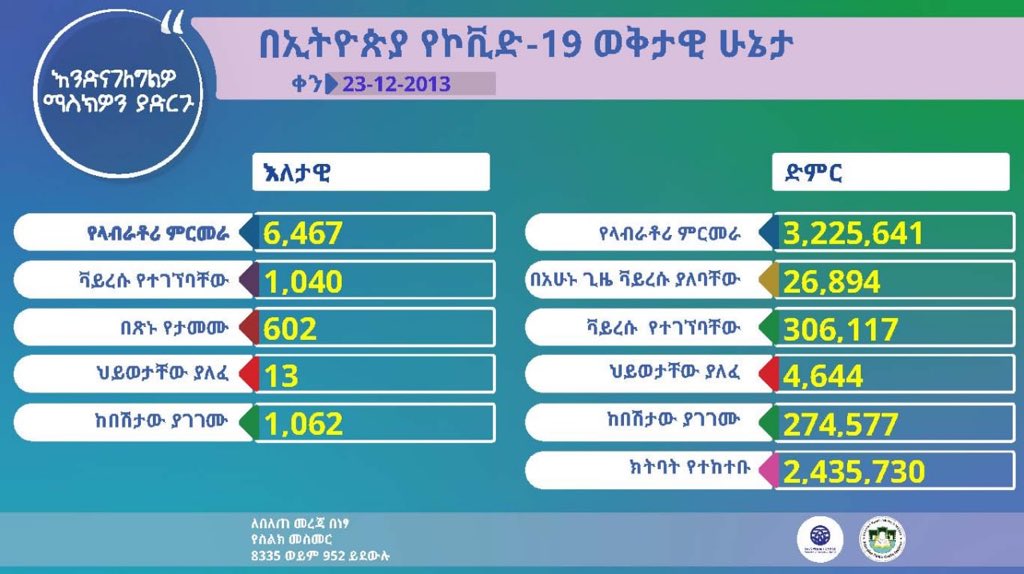
አደገኛው የኮቪድ ዴልታ ዝርያ ኢትዮጵያ ውስጥ መገኘቱን የጤና ሚኒስቴር ይፋ አደረገ።
የጤና ሚኒስትር ዶክተር ሊያ ታደሰ በሰጡት መግለጫ “በኢትዮጵያ ባለፉት ሳምንታት በወረርሽኙ የሚያዙ ሰዎች፣ የሚሞቱና ፅኑ ህሙማን ቁጥር በጣም አሻቅቧል” ብለዋል።
አዲሱ ዝርያ ሁሉንም የዕድሜ ክልል የሚያጠቃ፣ ለከባድ ህመምና ሞት የሚዳርግ በተለይም ባልተከተቡ ሰዎች ላይ የሚበረታ ዝርያ መሆኑን ገልፀዋል።
READ MORE -
https://mereja.com/amharic/v2/584132